How to Use a Soroban Abacus

The soroban abacus is a powerful calculating tool rooted in over 500 years of history. It is still used to this day for its practicality as well as its educational value for all ages and the visually impaired. After learning the basics of counting on the soroban abacus, you will be able to quickly perform arithmetic like addition, subtraction, multiplication, and division.

Counting
Adding and Subtracting
Multiplying
Dividing

Part 1 Counting

1. Position your abacus and default your beads

Abacus set that shows the default position for each column. All of the top row beads are in the up position, and down in the bottom row.

Each column has one bead in the top row, and four beads in the bottom. All of the top row beads should be in the up position, and down in the bottom row. This is the default position for each column. Each bead in the top row represents a value of 5 and each bead in the bottom row represents a value of 1.

2. Assign each column a place value

Abacus set with place value labels. Starting from the right are the "ones" place, to its left is the "tens" place, followed by the “hundreds”, “thousands” and so on.

Each column of beads represents a place value. Starting from the right are the "ones" place, to its left is the "tens" place, followed by the “hundreds”, “thousands” and so on.

You can also assign columns to be decimal places. For example, if you are representing a number like 12.5, then the furthest right column would be the “tenths” place (the first decimal place), to its left would be the “ones” place, followed by the “tens” place.

Likewise, to represent a number like 12.55, the furthest right column would be the “hundredths” place, to its left would be the “tenths” place, followed by the “ones” place, and then the “tens” place.

3. Counting 1 to 4 in the bottom row

Abacus set that shows how to count 1 to 4 in the bottom row. The number "one" is represented by a single bead pushed up from the bottom row. Number "two" is represented by 2 beads pushed up.

Start with the “ones” column. The number "one" would be represented by pushing up a single bead from the bottom row, where each bead represents a value of 1. Push up two beads for "two", etc.

A pro tip for speedy arithmetic: use your thumb to manipulate beads in the bottom row and your index finger for beads in the top.

4. Counting 5 to 9 using both rows

Abacus set that shows how to count 1 to 4 in the bottom row and how to count 5 and 6 using both rows.

The top row bead represents a value of 5. To indicate the number “five”, push the bead from the top row to the "down" position (a value of 5), and push all four beads from the bottom row down (a value of 0), for a total value of 5.

To count to "six," push one bead from the bottom row up. Together the top row (a value of 5) and the bottom row (a value of 1), this represents a total value of 6. Push up additional beads from the bottom row to continue the count.

5. Repeat the pattern for each place value

The process is the same across the abacus to indicate a digit for each place value.

To go from "nine” to "ten”, the ones column is set to the default position of “zero” (top row bead up, bottom row beads down), and the tens column is set to “one” (top row bead up, one bead up in the bottom row). Reading the abacus left to right would be the digits 1, 0, or “ten”.

“Eleven” would have one bead from the bottom row in the tens column pushed up, and another bead from the bottom of the ones column pushed up. The digits would read 1, 1, or “eleven”

Continuing into the hundreds, thousands, and so on, simply position 0 to 9 in each place column to indicate the digit of the place value.

Part 2 Adding and Subtracting

1. Line up your first number

2,145 is entered in the abacus. Top row bead in the “ones” column is pushed down. Four bottom row beads in the “tens”, one in the “hundreds”, and two in the “thousands” are pushed up.

Let’s add 2,145 and 5,668. First reset your abacaus to default position. Then enter 2,145 on the abacus by pushing down a top row bead in the “ones” column, push up four bottom row beads in the “tens”, one in the “hundreds”, and two in the “thousands”.

2. Start adding from the largest place value

Abacus shows the addition process of 2+5=7 from the "thousands" column and 1+6=7 from the "hundreds" column.

The first numbers you'll add are the 5 to the 2 from the “thousands” column. Push a single bead from the top row of that column down and keep the two beads from the bottom row up. The “thousands” column is now a 7 digit.

Likewise, add 6 to the 1 in the hundreds place. Move the top row bead in the “hundreds” column down and push another bottom row bead up to for a 7 digit.

3. Carrying over

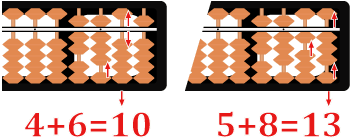
Abacus shows the addition process of 4+6=10 from the "tens" column and 5+8=13 from the "ones" column.

Adding 6 to the 4 in the “tens” column will result in 10. You'll carry over a 1 to the “hundreds”, making the 7 an 8 in that column. Next, push all the beads down in the “tens”, making the digit a 0.

In the ones column, 5 plus 8 equals 13, so you'll carry a 1 over to the “tens” column, making the 0 digit a 1. Push the top row bead up in the “ones” column, and three beads up from the bottom, making the “ones” column digit a 3.

4. Read the columns to get the answer

Abacus shows a 7 in the “thousands” column, an 8 in the “hundreds”, a 1 in the “tens”, and a 3 in the “ones”.

To recap, you now have a 7 in the “thousands” column, an 8 in the “hundreds”, a 1 in the “tens”, and a 3 in the “ones”: 2,145 + 5,668 = 7,813.

5. Subtract by doing the process in reverse

Abacus shows how to subract 788 from 845. 845 is entered on the abacus. Subtraction starts from the largest place value column.

Let’s subract 788 from 845. Enter 845 on the abacus and start subtracting from the largest place value column and borrow digits from the previous column instead of carrying them over.

• 7 from 8 is 1, so move the top row bead up and leave a single bead from the bottom row up in the hundreds place.
• In the tens place, you can't subtract 8 from 4, so you'll borrow the 1 in the hundreds place (leaving it zero) and subtract 8 from 14, making it 6 in the tens place (one bead down in the top row and one bead up in the lower).
• Do the same in the ones place, "borrowing" a bead from the tens place making the tens place go from a 6 to a 5. Subtract 8 from 15 making the ones place a 7.
• Read the answer to 845 - 788, from left to right: 57.

Part 3 Multiplying

1.Record the problem

Abacus shows how to multiply 43 and 13. Starting at the furthest left column of the abacus, columns are assigned to "4", "3", default position for "x", "1", "3", and default position for "=".

Let’s multiply 43 and 13. Start at the furthest left column of the abacus and assign columns to "4", "3", default position for "x", "1", "3", and default position for "=". Leave the remaining columns in the default position as well for recording the solution.

2.Multiply by alternating columns

Abacus shows how to multiply each digit in the problem in an alternating column sequence.

Multiplication is broken down by multiplying each digit in the problem in an alternating column sequence:

a) Multiply the tens column by the tens column after the x.
b) Multiply the tens column by the ones column after the x.
c) Multiply the ones column by the tens column after the x.
d) Multiply the ones column by the ones column after the x.

For multiplying numbers with more place values, follow the same pattern of starting with the leftmost digits, and working to the right.

3. Record the products

Abacus shows how to record the product of the alternating column multiplication in the answer columns, starting after the "=" column.

Record the product of the alternating column multiplication in the answer columns, starting after the "=" column. For the problem 43 x 13:

a) Multiply 4 and 1, recording the product 4 in the first answer column. Push four bottom row beads up in that seventh column.
b) Multiply 4 and 3, recording the product 12 in the eighth column. Push two bottom row beads up to record a 2. Carry over a 1 to the previous seventh column, changing the digit from a 4 to a 5 by pushing the top row bead and all the bottom row beads down.
c) Multiply 3 and 1, recording the product 3 in the eighth column by adding it to the existing 2. 3 + 2 = 5. Push the top row bead down and all the bottom row beads down, for the digit 5.
d) Multiply 3 and 3, recording the product 9 in the ninth column. Push the top row bead down and all the bottom row beads up.

Read your answer from left to right in the product columns after the “=”: 559.

Part 4 Dividing

1. Record the problem

Abacus shows the recording arrangement for the sample division problem 78÷3. Recording starts from the furthest left column, which is the divisor, followed by quotient, and then the dividend.

Let’s divide 78 by 3. The recording arrangement starting from the furthest left column is the divisor, followed by quotient, and then the dividend:

• In the furthest left column assign the divisor “3”.
• Moving to the right, leave the quotient columns in default position. The number of columns for the quotient should be the number of places in the dividend. In this case the dividend is 78, which has two places, therefore leave two columns in default position.
• Following the quotient columns, record the dividend columns 7 and 8.
• If you like, you can add an additional column in default position between the divisor and the quotient columns, and between the dividend and quotient columns. This can help you distinguish the quotient as you work through the problem.

2. Record the first quotient digit

Abacus shows how to record the first quotient digit. Two bottom row beads are pushed up in the first quotient column.

Divide the first number in the dividend (7) by the divisor (3), and put it in the first quotient column. 3 goes into 7 twice, so record a 2 there. Push two bottom row beads up in the first quotient column.

3. Determine the remainder and record

Abacus shows how to multiply the quotient in the first quotient column (2) by the first divisor column (3). The product (6) needs to be subtracted from the first dividend column (7), to get the remainder (1). The top row bead up is pushed up and one bottom row bead is left up, so that the 7 becomes a 1. The dividend columns now reads 18.

Next, multiply the quotient in the first quotient column (2) by the first divisor column (3). The product (6) needs to be subtracted from the first dividend column (7), to get the remainder (1). Push the top row bead up and leave one bottom row bead up, so that the 7 becomes a 1. The dividend columns should now read 18.

4. Repeat the process

Abacus shows how to record the next digit of the quotient.

Record the next digit of the quotient, by dividing the next number in the dividend including the remainder to its left (18) by the divisor (3). 18 divided by 3 is 6.

• In the second quotient column, push up one top row bead down and one bottom row bead up, for the digit 6.
• Read your quotient from left to right to get your answer: 26.